PROC FREQ : 범주형 자료(명목형, 순서형)로 구성된 분할표를 작성하거나, 교차분석을 하기 위함
* 범주형 자료 : 관측값의 크기 보단, 포함되는 범주에 관심을 가짐.-> 도수분포표나 분할표로 표현
범주형 자료 분석
1) 적합도 검정 :
크기 n의 관측치를 m개의 범주로 분류했을 때, 각 관측치들이 각각의 그룹에 속할 확률이 알려져있는 경우,
실제로 이러한 형태대로 관측값들이 분류되었는지 검정
2) 독립성 검정 :
두개의 변수가 서로 상관이 있는가? 연관이 있는가? 서로 독립인가?
행변수와 열변수 간의 독립성 여부 검정 ( 카이제곱 통계량에 기초)
EX) H0 : A와 B는 서로 상관관계가 없다 = 독립이다
H1 : A와 B는 서로 상관이 있다.
3) 동질성 검정 :
두 개의 변수의 확률이 서로 같은가? 차이가 없는가?
사전연구(prospective study)에 사용. 한쪽 주변합 고정(one-margin fixed)
EX) HO : A와 B를 선택하는 확률에는 차이가 없다 = 같다.
H1 : A와 B를 선택하는 확률에는 차이가 있다.
형식 :
PROC FREQ DATA=데이터셋명 ;
BY 변수이름;
EXACT 키워드/선택사항; /* 데이터들에 대한 정확성 검증을 수행*/;
OUTPUT OUT=데이터셋명;
TEST 선택사항; /* 연관성 척도와 동일성 척도에 대한 검증을 수행*/;
TABLES 변수이름 [변수이름1*변수이름2] /선택사항; /*범주형 변수 입력*/;
WEIGHT 변수이름/옵션; /* FREQ 절차에 포함되는 자료의 가중치변수 지정*/;
RUN;
# 분할표
: 카이제곱 검정 : 행변수와 열변수 간의 독립성 여부 검정 / P-VALUE 검정
분할표 만들기
PROC FREQ data=htwt;
TABLES dept gender*dept;
RUN;
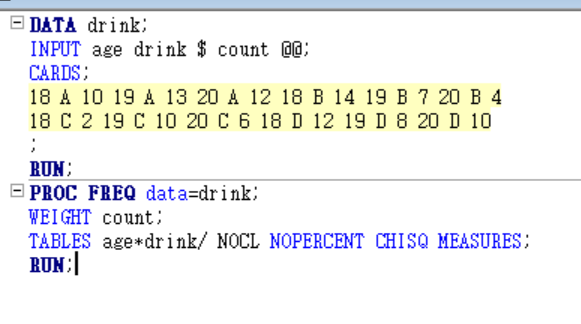
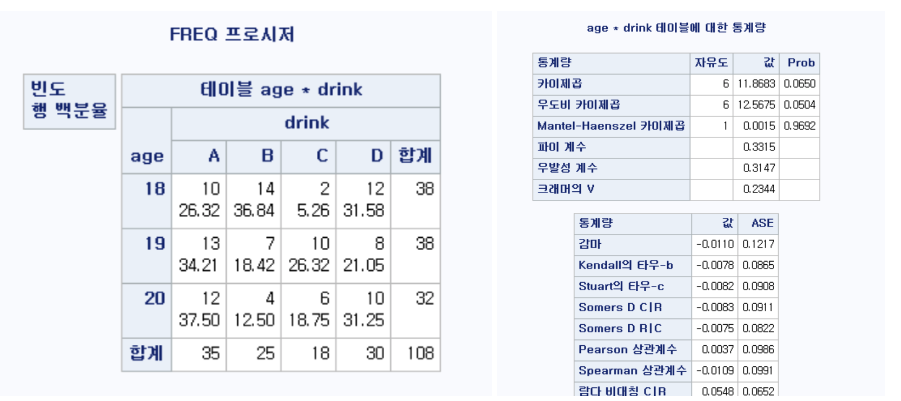
-> 4x3 분할표 완성
-> 카이제곱 p-value 가 0.065 >0.05 이므로 귀무가설 기각 x -> 차이가 없다.
1) 적합도 예시
ex)주사위를 던졌을 때 확률 1/6 이 그대로 나오는지


-> 여기서 p-value 가 0.9로 매우 높으므로 기각x -> 결론 : 차이가 없다. 그대로 나온다!
2) 독립성 예시
ex) 경제력에 따라 쇼핑장소에 차이가 있는가?


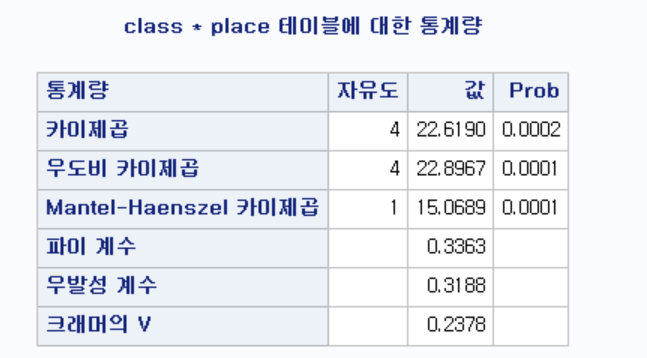
-> 여기서 p-value 가 매우 작기 때문에 귀무가설을 기각!
-> 결론 : 차이가 있다.
3) 동질성 예시
ex) 성별에 따라 전공을 선택하는데 차이가 있는가?
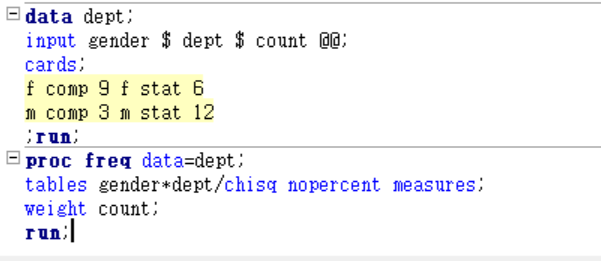


여기서, 남자(m) 이면서 컴퓨터학과(comp)의 수가 5미만이면서 25% 미만으로 나오기 때문에
카이 제곱 검정 통계량으로 확인하면 x
-> FISHER 검정으로 확인 !!
결과 : 귀무가설 기각X .차이가 없다.
PROC BOXPLOT : 자료의 퍼짐 정도를 그래프로 표현
PROC SORT DATA=데이터셋 명;
BY 변수이름 ; RUN;
해주고
PROC BOXPLOT DATA=데이터셋명 선택사항;
BY 변수이름;
ID 변수이름;
PLOT 변수이름* 그룹변수이름/선택사항;
RUN;
'데이터 스터디 > SAS' 카테고리의 다른 글
| SAS - 데이터 요약과 표현 (PROC PRINT, MEANS, UNIVARIATE) (0) | 2023.03.22 |
|---|---|
| SAS - 데이터 셋의 결합 및 관리 (merge, do-loop문, 자동변수, 외부파일 put문) (0) | 2023.03.22 |
| SAS - 명령문 (if 조건문,retain, array) (0) | 2023.03.22 |
| SAS - 구분자(dlm, dsd) , 할당문, 날짜함수 (0) | 2023.03.22 |
| SAS - 변수 속성 할당 (0) | 2023.03.22 |