05. Loss function(손실함수) - 회귀&분류
이때까지 입이 닳도록 말해온 것이 바로,
예측값과 실제값 사이의 차이, 즉 LOSS를 최소화하는 방향으로 학습은 진행되어야한다.
loss function과 cost function, 그리고 이들을 아우르는 objective function은 이전 글에서 다룬 적도 있다.
[물음표/느낌표] 01. cost function과 loss function 차이
[물음표/느낌표] 01. cost function과 loss function 차이 우리는 앞서 머신러닝에선 손실, 즉 loss function을 최소화하는 방향으로 학습해야한다는 것을 알았다. 이때 많이들 혼란스러워하는 용어가 바
uumini.tistory.com
정리하자면, 통계적 머신러닝의 목적은 이 손실함수를 최소화함으로써 , 우리가 모르는 선형회귀식/분류 방정식 속의 모수 베타들을 추정하여 실제와 비슷한 y값을 예측하는 것이다.
이때 회귀와 분류의 방식은 살짝 다르다.
- 회귀의 경우, 회귀에서는 추정한 베타를 통해 연속형 수치인 y를 정확히 바로 예측하는데 쓸 수 있지만
- 분류의 경우, 우리는 범주형 값인 y를 예측해야하기에 1) 베타를 추정하여 만들어진 선형함수를 2) sigmoid(=이중분류) /softmax(= 다중분류) 함수에 넣어서 3) 추정확률을 구하고 4) 해당 확률이 어느 label에 가까운지 할당하는 방식을 취한다.
마찬가지로 손실함수의 종류도 회귀(regression)와 분류(classification)에 따라서 다르다.
- 회귀의 경우, 대표적 손실 함수는 MAE, MSE, RMSE 가 있다
- 분류의 경우, Binary cross-entropy, Categorical cross-entropy 등이 있다.
❕ 손실함수 종류 - 회귀 ❕
1. 평균 절대 오차 (Mean Absolute Error, MAE)
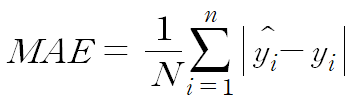
- 예측 값과 정답 값의 차이에 절댓값 -> 그 값들을 전부 더하고 -> 개수 N으로 나누어 평균을 낸 값
- 예측 결과와 정답 결과가 떨어진 정도의 절댓값을 평균 낸 것이기에, 전체 데이터의 학습된 정도를 쉽게 파악 가능
- 절대값 때문에 어떤 식으로 오차가 발생했는지, 음수인지 양수인지 판단할 수 없다
- 또한 아래 그림처럼 최적의 값에 가까워지더라도 이동거리가 일정하기 때문에 최적의 값에 수렴하기 어렵다.
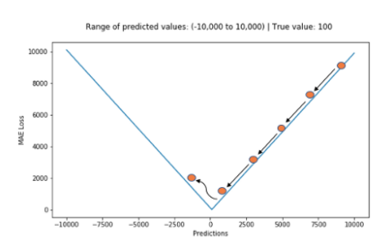
2. 평균 제곱 오차 (Mean Squared Error, MSE)

- 가장 많이 쓰이는 손실 함수 중 하나
- 예측 값과 실제 값 사이의 평균을 제곱하여 평균을 낸 값
- 제곱 연산으로 인해 차이가 커질수록 MSE값이 뚜렷해지며 제곱으로 인해 오차가 양수든 음수든 누적 값을 증가시킴
- 하지만 제곱으로 인해 "1 미만의 값은 더 작아지고, 그 이상의 값은 더 커진다”, 즉 값의 왜곡 발생
- MAE와 달리 최적 값에 가까워질 경우 (함수가 convex 굴곡형태이기 때문!!) 이동거리가 다르게 변화하기 때문에 최적 값에 수렴하기 용이하다
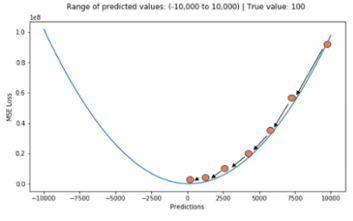
3. 평균 제곱근 오차(Root Mean Square Error, RMSE)
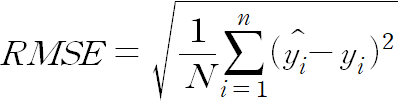
- MSE에서 값을 제곱해서 생기는 왜곡이 줄어들며, 오차를 보다 직관적으로 보여줌
❕ 손실함수 종류 - 분류 ❕
- 대표적인 손실함수로 cross-entropy 방식
- Cross-entropy는 실제 label인 y_i에 대하여 이들의 실제 확률분포를 알지 못하는 상태에서, 모델링을 통하여 구한 확률 p를 통하여 y가 0인지 1인지, 혹은 다른 multi 범주에 해당하는 애인지를 예측하는 것이다.
- 이때 Cross-entropy는 label의 값을 one-hot-encoding의 방식일 경우에만 사용가능하다.
*One hot encoding: multinomial classification에서 사용하는 인코딩 방법으로 출력 값의 형태가 정답 label은 1이고 나머지 label 값은 모두 0 ex) [1,0,0], [0,1,0], [0,0,1]
- The more we are away from our target, the more the error grows
이때, y_i와 p가 모두 식에 들어가기 때문에, cross-entropy라는 이름이 생겼다.
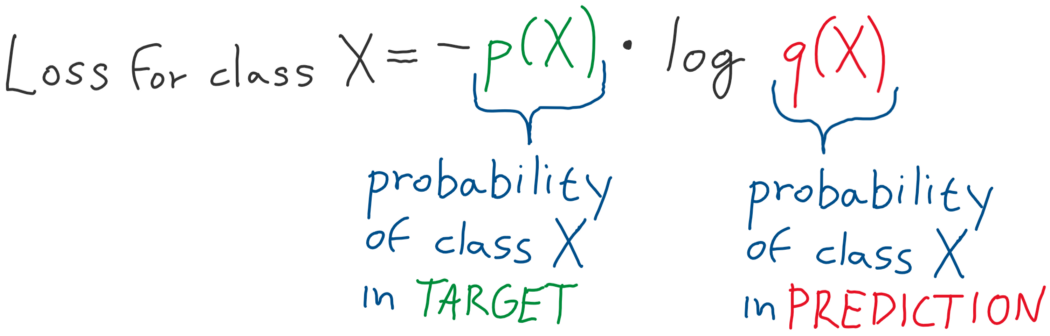

그렇다면 이제 Binary cross-entropy와 Categorical cross-entropy 식을 알아보겠다.
1. Binary cross-entropy
- Binary cross-entropy는 이진 분류에 사용되는 방식

2. Categorical cross-entropy
- Categorical cross-entropy는 분류해야 할 클래스가 3개 이상인 경우, 즉 멀티클래스 분류에 사용
- 라벨이 [0,0,1,0,0], [1,0,0,0,0], [0,0,0,1,0]과 같이 one-hot 형태로 제공될 때 사용됩니다. 일반적으로 예측 값은 [0.02 0.94 0.02 0.01 0.01]와 같은 식으로 나오기 때문에 여러 class 중 가장 적절한 하나의 class를 분류하는 문제에 사용

그리고 이들을 얻게 되는 과정은 아래와 같다.

❕ 손실함수 최적화 - 경사하강법 ?❕
분류에 사용되는 손실함수인 cross entropy의 경우, 회귀의 손실함수처럼 파라미터를 추정하기 위해 각 βj에 대해 편미분한 ∂f/∂βj 식을 0으로 두고 미분방정식을 푸는 방법과는 달리, 그렇게 간단한 형태가 아니다.
따라서 손실함수를 최소화하는 모수 베타를 구하기 위하여 회귀의 LSE방식이 아닌 최적화 방식을 사용한다. 경사 하강법(gradient descent)과 같은 방법 말이다. 이에 대한 내용을 다음 포스팅에서 다루도록 하겠다.
❗ 정리하자면 ❗
- -regression은 정규분포를 따른다는 가정 하에 선형모형을 만들고
- -logistic regression은 베르누이분포를 따른다는 가정 하에 해당하는 p_i부분을 로짓변환해서 선형모형을 만든다. (이때 로짓변환을 하는 이유는 (-무한대 , +무한대)까지로 두기 위해
-loss function의 대략적인 종류
- -regression -> SSE
- -logistic regression -> Cross Entropy

'데이터 스터디 > Stats\ML' 카테고리의 다른 글
| [?!] learning rate (0) | 2022.02.28 |
|---|---|
| 06. Gradient Descent (0) | 2022.02.27 |
| 04-2. Regression(회귀) - 로지스틱회귀 (0) | 2022.02.18 |
| 04-1. Regression(회귀) - 선형회귀 (0) | 2022.02.12 |
| [?!] cost function과 loss function 차이 (0) | 2022.02.11 |