앞서서 Loss Function에 대해 알아보았다.
이젠 Regression과 Classification 모델들의 Loss Function을 Optimization 하는 방법을 알아보자.
*최적화(optimization) 란 어떤 목적함수(objective function)의 함수값을 최적화(최대화 또는 최소화)시키는 파라미터(변수) 조합을 찾는 문제를 말한다.
06. Gradient Descent
만약 선형모형처럼 손실함수가 1차함수, 2차함수로 간단히 표현되는 경우라면 한 파라미터에 대해 미분해서 0이 되는 지점을 찾아 최소값을 바로 찾을 수 있다. 하지만, 우리가 마주치는 손실함수(cross entropy 등)는 간단한 형태가 아니어서 미분방정식을 푸는데 한계가 있다. 명확한 해답이 없기에 수치적 접근으로 다가가야한다.
=> Some problems do not have an explicit solution and a numerical approach should be exploited
따라서 최적화를 진행하는 방법으로, 근사값을 이용하는 방법인 Newton-Raphson Method와 Gradient Descent 방법이 있다.
이때 Newton-Raphson Method에서 Hessian의 inverse값을 구하는게 힘들기 때문에 Gradient Descent 방법을 주로 사용한다.
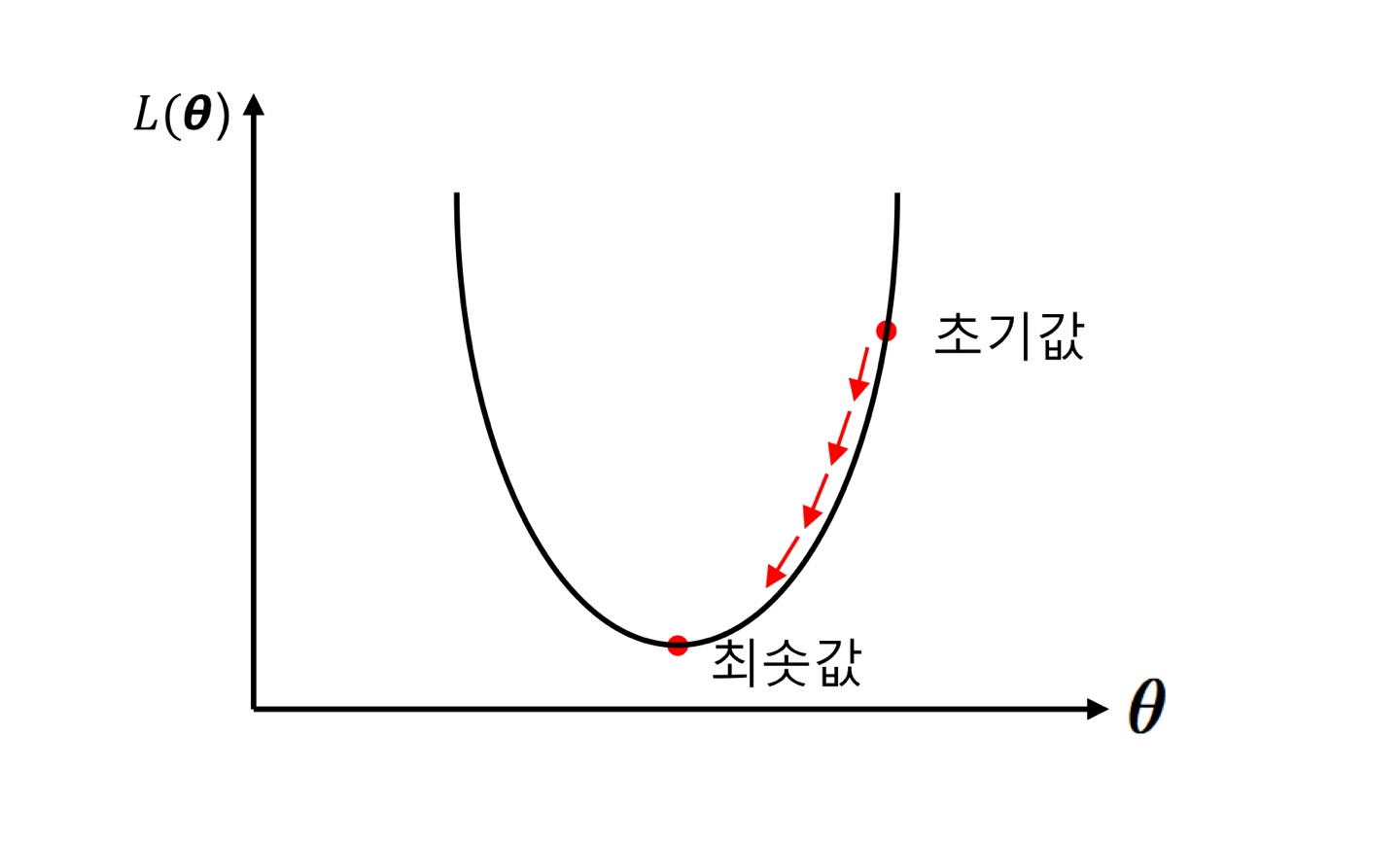
미분했을 때 나오는 값의 반대 방향으로, 즉 양수가 나온다면 더 줄어드는 방향으로 파라미터를 조정해가는 것이 바로 경사하강법이다.
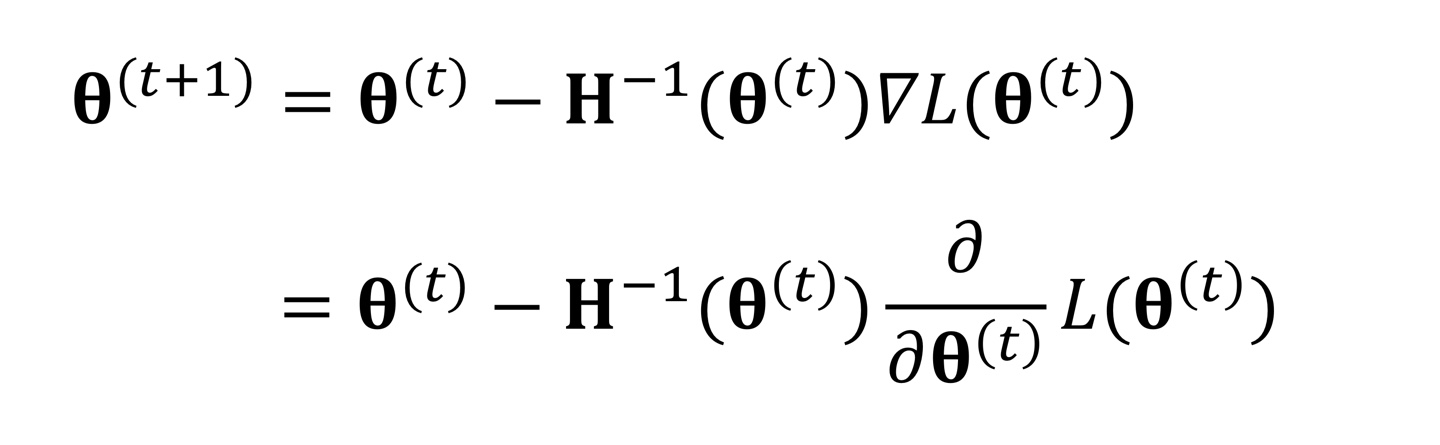
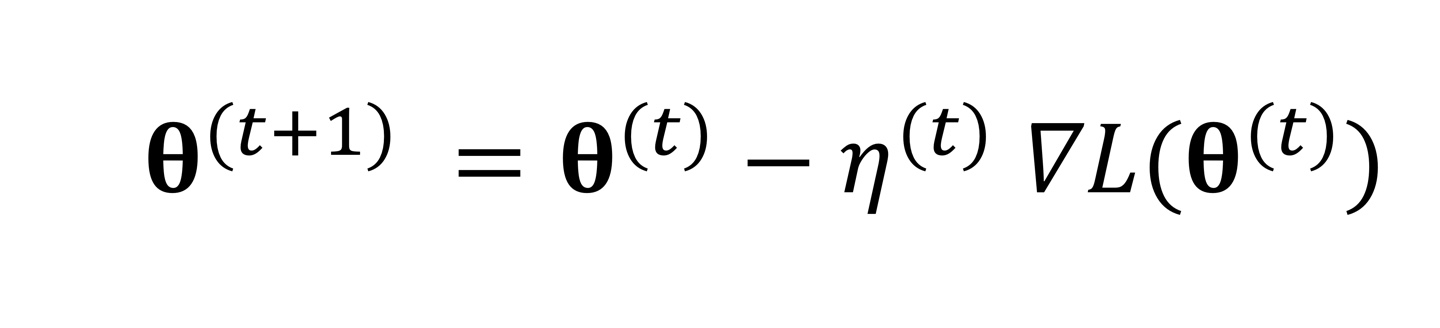
식을 보면 Hessian의 inverse값 대신에 learning rate이 들어가고 있다.
❕ 배치 경사 하강법(Batch gradient descent) ❕

경사하강법을 설명할 땐 등산에 비유를 자주한다.
배치 경사 하강법에서는 한 스텝 한 스텝 이동할 때마다 최소값으로 다가가기 위한 최적화가 이루어지는데, 이때마다 각 지점에서의 기울기를 우리는 구하는 번거로움이 생긴다.
다시 있어보이게 말하자면 파라미터 θ가 바뀔 때마다 손실함수의 결과 값이 얼마나 바뀌는지 그래디언트 벡터(gradient vector)를 측정해야 한다. 그래디언트 벡터는 파라미터 θ에 대한 손실함수의 편도함수(partial derivative), 즉 해당 지점에서의 기울기이다. 따라서 배치 경사 하강법의 가장 큰 특징이자 단점은 파라미터가 바뀔 때마다 모든 데이터의 편도함수를 계산한다는 것입니다. 이 때문에 전체 훈련 세트가 커지면 계산 속도가 매우 느려진다는 단점이 있다.
단점 1. Batch 전체를 구하기에 계산속도가 매우 느리다.
단점 2. 데이터 전체를 대상으로 하기 때문에 중간에 데이터가 뒤늦게 추가된다면 최적화 단계에 포함되지 x.
❕ 확률적 경사 하강법 (Stochastic gradient descent) ❕
모든 데이터를 대상으로 global minimum 사냥에 나섰던 배치 경사 하강법과 달리,
확률적 경사 하강법은 이름처럼 매 스텝에서 확률적으로 !! 즉, random하게!! 무작위로 한 개의 데이터를 선택하고, 그 데이터값에 대한 그래디언트 벡터(gradient vector)만을 계산한다.

먼저 데이터를 셔플한 다음에 첫번째 데이터에 대해서 미분을 시켜서 파라미터를 업데이트시키고(1 iteration), 다음 데이터로 파라미터를 업데이트시키고 ,, ~ 이런 작업을 데이터를 다 쓸 때까지, 즉 1 epoch까지 돌리게 된다. 따라서 매번 적은 데이터를 처리하기 때문에 전체 훈련 세트의 크기가 크더라도 어렵지 않게 훈련시킬 수 있다.
또한 무작위로 움직인다는 점에서 local minimum에 빠질 위험이 훨씬 줄어든다. 다른 데이터를 사용하면서 local minimum에서 빠져나올 수 있기 때문이다. 하지만 엄밀하게 움직이지 않기 때문에 정확한 global minimum에 도달하기 어렵다는 단점이 있다. 이 딜레마를 해결하기 위해서 초반에는 학습률을 크게 설정해서 지역 최소값에 빠지지 않게 하고, 점진적으로 학습률을 줄여가면서 전역 최소값에 도달하게 하는 방법을 사용하기도 한다. (learning rate annealing)
❕ 미니배치 경사 하강법(Mini-batch gradient descent) ❕
미니배치 경사 하강법은 앞선 배치 경사 하강법(batch-gradient descent)과 확률적 경사 하강법(SGD)의 장단점을 종합한 방법으로, 실제로 가장 많이 사용되는 방법이다.
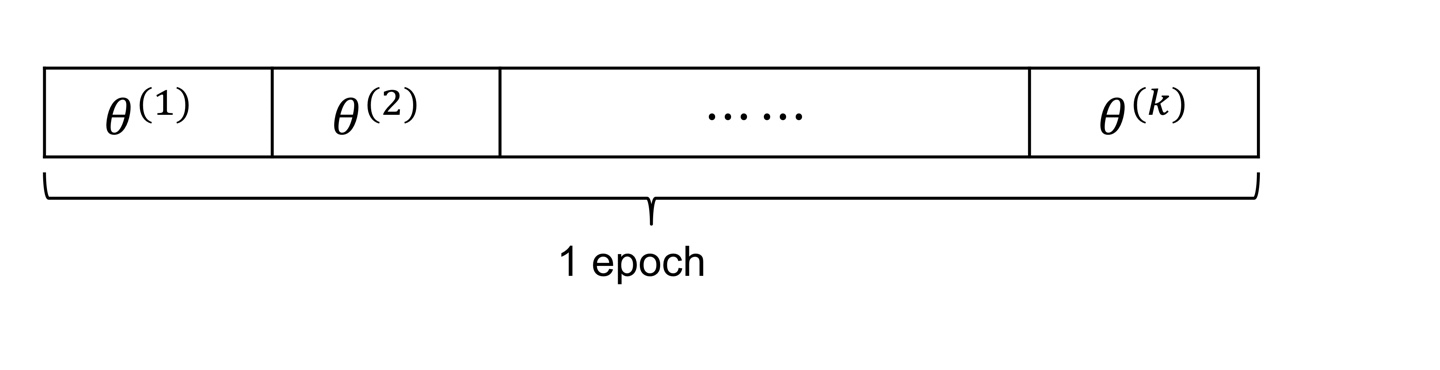
미니배치 경사 하강법에서는 전체 데이터셋에서 일정하게 등분한 sample 데이터셋(미니배치)에 대한 그래디언트 벡터(gradient vector)를 계산한다. 예를 들어 batch_size = 8 이라는 것은, 전체 데이터셋에서 8개를 한번에 계산하여 최적화하겠다는 의미이다. (확률적 경사 하강법은 그렇다면 배치 사이즈가 1인 것을 말한다)
'데이터 스터디 > Stats\ML' 카테고리의 다른 글
| 07. 과적합(Overfitting)과 정규화(Regularization) (0) | 2022.03.04 |
|---|---|
| [?!] learning rate (0) | 2022.02.28 |
| 05. Loss function(손실함수) - 회귀&분류 (0) | 2022.02.19 |
| 04-2. Regression(회귀) - 로지스틱회귀 (0) | 2022.02.18 |
| 04-1. Regression(회귀) - 선형회귀 (0) | 2022.02.12 |