07. 과적합(Overfitting)과 정규화(Regularization)
07. 과적합(Overfitting)과 정규화(Regularization) ❕ 오버피팅을 조심하자 ❕ (feature 수가 너무 많아서와 같은 이유로) 모델이 복잡해 variance가 커진 것을 오버피팅 overfitting 이라고 부른다. 우리가 모..
uumini.tistory.com
앞서 오버피팅과 정규화의 원리에 대해 알아보았다.
이번엔 정규화 중 L2-norm 형식을 살펴보자.
❕ 정규화 (1) - L2 정규화 : Ridge regression ❕

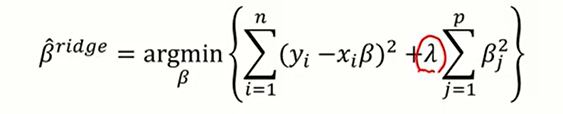
L2 정규화는 "회귀 계수 β에 대한 제곱값"에 대한 제약조건을 취한 것이다.
그리고 이를 선형 회귀모델에 적용한 것이 Ridge regression이다.
Ridge regression에선 mse를 최소화 시키는 와중에 계수값에 대한 제곱을 특정 값(t)보다 작게 하자는 제약을 가하고 있다. (베타에다가 제약을 주지 않으면 LSE가 만족해 가장 좋은 값이 될 것이다. )
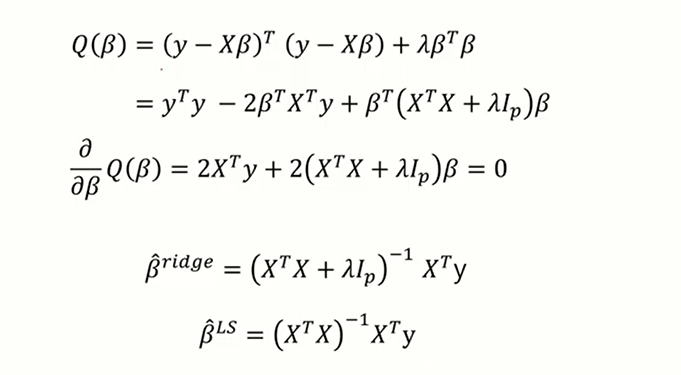
Ridge regression 의 목적함수(= 손실함수)는 위와 같이 표현할 수 있고 ,
이를 최소화함으로써 모수 베타를 추정한 값은 아래와 같다.
(*최소화하는 방법은 여느때와 다름없이 베타에 대하여 미분한 후 =0으로 셋팅해 풀어준다)
그렇다면 이때 t, 또는 λ의 크기는 어떻게 설정해야할까 ?

위의 그림을 참고하면서 설명해보겠다.
제약조건이 없는 경우 minimize cost 지점이 바로 LSE를 통해 구해낸 베타 β(회귀계수)이다.
하지만 제약조건을 가하게 된다면 제약조건에서 lse_β와 가장 근접한 지점인 rigde_β가 선택받게 된다. 이는 bias를 희생해서 variance를 줄이기 위한 작업이다.
이때 제약을 주는 lambda λ값을 크게 준다면 rigde_β가 lse_β보다 크기가 작아지면서 모수 베타가 0으로 쪼그라드는Shrinkage 현상이 생긴다. 0으로 줄어든다는 것은 결국 파라미터(=가중치)를 줄여 해당 X변수를 제거하다싶이 하는 것이고 이것이 바로 오버피팅을 막는 L2 정규화의 원리이다.
'데이터 스터디 > Stats\ML' 카테고리의 다른 글
| [코드 분석] Time Series Regression - Predict Future Sales 커널 필사 (0) | 2023.02.01 |
|---|---|
| 07. 과적합(Overfitting)과 정규화(Regularization) (0) | 2022.03.04 |
| [?!] learning rate (0) | 2022.02.28 |
| 06. Gradient Descent (0) | 2022.02.27 |
| 05. Loss function(손실함수) - 회귀&분류 (0) | 2022.02.19 |